Senior Lecturer in Mathematics
Department of Mathematics and Statistics
University of Exeter, Streatham Campus
Exeter EX4 4QF
ENGLAND

Resonance in Cooker's sloshing experiment
Cooker's sloshing experiment is a prototype for studying the dynamic coupling between fluid sloshing and vessel motion. It involves a container, partially filled with fluid, suspended by two cables and constrained to remain horizontal while undergoing a pendulum-like motion. In this paper the fully-nonlinear equations are taken as a starting point, including a new derivation of the coupled equation for vessel motion, which is a forced nonlinear pendulum equation. The equations are then linearized and the natural frequencies studied. The coupling leads to a highly nonlinear transcendental characteristic equation for the frequencies. Two derivations of the characteristic equation are given, one based on a cosine expansion and the other based on a class of vertical eigenfunctions. These two characteristic equations are compared with previous results in the literature. Although the two derivations lead to dramatically different forms for the characteristic equation, we prove that they are equivalent. The most important observation is the discovery of an internal 1:1 resonance in the fully two-dimensional finite depth model, where symmetric fluid modes are coupled to the vessel motion. Numerical evaluation of the resonant and nonresonant modes are presented. The implications of the resonance for the fluid dynamics, and for the nonlinear coupled dynamics near the resonance are also briefly discussed.

Alemi Ardakani H, Bridges TJ, Turner MR. (2012) Resonance in a model for Cooker's sloshing experiment, European Journal of Mechanics,B/Fluids, volume 36, pages 25-38, DOI:10.1016/j.euromechflu.2012.04.007.
H. Alemi Ardakani, T.J. Bridges & M.R. Turner. Resonance in a model for Cooker's sloshing experiment (the extended version,) Technical Report (2012) [PDF]
H. Alemi Ardakani. (2010) Rigid-body motion with interior shallow-water sloshing, Ph.D. Thesis, University of Surrey, UK.
H. Alemi Ardakani. (2010) Symplecticity of the Stormer-Verlet algorithm for dynamic coupling between shallow-water sloshing and vehicle motion in horizontal plane, Department of Mathematics, University of Surrey. [PDF]
M.R. Turner & T.J. Bridges. Nonlinear energy transfer between fluid sloshing and vessel motion, J. Fluid Mech. 719, 606-636 (2013) [PDF]
Proof of equivalence
The boundary-value problem for the linear horizontally-forced sloshing problem can be solved using two different classes of eigenfunction expansions. The first will be referred to as the "cosine" expansion since the organizing centre is a cosine series in the x-direction (the horizontal direction), and the second is called the "vertical eigenfunction expansion'' since the organizing centre is a class of y-direction (the vertical direction) eigenfunctions. These two methods lead to very different forms of solution, and their equivalence is not obvious. This technical report gives the details of a proof of equivalence. The strategy of the proof was suggested to the authors by Phil McIver (Loughborough).

H. Alemi Ardakani, T.J. Bridges & M.R. Turner. Details of the proof of equivalence: the "cosine'' versus "vertical eigenfunction'' representations. Technical Report (2012) [PDF]
1:1 resonance in shallow water
In this report an explicit proof is given showing how the 1:1 resonance arises in the shallow water model for dynamic coupling in Cooker's sloshing experiment.
H. Alemi Ardakani & T.J. Bridges. 1:1 resonance in the shallow-water model for Cooker's sloshing experiment. Technical Report (2011) [PDF]

Baffling and a multifold 1:---:1 resonance
Strong internal resonance, or 1:1 resonance, in a linearized model for a physical system is a precursor to dramatic dynamics in the nonlinear problem. Such resonances have been found in fluid models, mechanical systems and in celestial mechanics. It is generally believed that higher order, 1:1:1 or 1:1:1:1 internal resonances are rare. However, we have discovered a physical system that has an (n+1)-fold 1: --- :1 resonance for any natural number n. These resonances occur at natural parameter values and an experimental configuration is constructible. Moreover, the system is of great practical importance as it is a model for dynamic coupling between vessel motion and fluid sloshing for a container with baffles.

Turner MR, Bridges TJ, Alemi Ardakani H. (2013) Dynamic coupling in Cooker's sloshing experiment with baffles, Physics of Fluids, volume 25, no. 11, pages 112102-112102, DOI:10.1063/1.4827203.
Lagrangian particle path formulation of multilayer shallow-water flows
dynamically coupled to vessel motion
The coupled motion—between multiple inviscid, incompressible, immiscible fluid layers in a rectangular vessel with a rigid lid and the vessel dynamics—is considered. The fluid layers are assumed to be thin and the shallow-water assumption is applied. The governing form of the Lagrangian functional in the Lagrangian particle path (LPP) framework is derived for an arbitrary number of layers, while the corresponding Hamiltonian is explicitly derived in the case of two- and three-layer fluids. The Hamiltonian formulation has nice properties for numerical simulations, and a fast, effective and symplectic numerical scheme is presented in the two- and three-layer cases, based upon the implicit-midpoint rule. Results of the simulations are compared with linear solutions and with the existing results of Alemi Ardakani et al. (J Fluid Struct 59:432–460, 2015) which were obtained using a finite volume approach in the Eulerian representation. The latter results are extended to non-Boussinesq regimes. The advantages and limitations of the LPP formulation and variational discretization are highlighted.
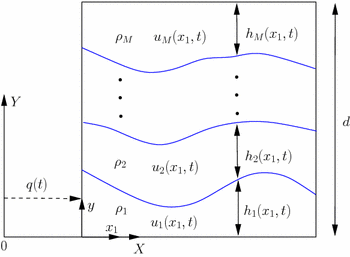
Turner MR, Bridges TJ, Alemi Ardakani H. (2017) Lagrangian particle path formulation of multilayer shallow-water flows dynamically coupled to vessel motion, Journal of Engineering Mathematics, volume 106, no. 1, pages 75-106, DOI:10.1007/s10665-016-9893-3. [PDF]

