Senior Lecturer in Mathematics
Department of Mathematics and Statistics
University of Exeter, Streatham Campus
Exeter EX4 4QF
ENGLAND

Shallow water sloshing in 3D rotating vessels
Details of the numerical algorithm used to solve the rotating shallow water equations (SWEs) are recorded in the report below, and the Matlab code is available for downloading. The equations are derived in J. Fluid Mech. 667 474-519 (2011). The numerical scheme is a fully-implicit split-step scheme with second order accuracy in both space and time that has been widely used in hydraulics. The nonlinearity is treated in the Eulerian representation using iteration. The new features in the algorithm here are (a) the inclusion of full time-dependent rotation due to the rigid body motion of the vessel, and (b) the use of exact boundary conditions in both steps of the split-step scheme. In Section 2 of the report the algorithm for the SWEs in one space dimension is outlined. This algorithm is a streamlined version of the algorithm used in the 3D numerics. The simplification introduced here is that the nonlinear term is replaced by the linear term, using mass conservation, in the U-momentum equation.


H. Alemi Ardakani & T.J. Bridges. Shallow water sloshing in rotating vessels: details of the numerical algorithm, Internal Report [PDF]
Matlab codes for 2D forced sloshing
This Matlab code solves the new shallow-water equations, for sloshing in two dimensions (one horizontal and one vertical) in a vessel which is undergoing rigid-body motion in the plane, derived in Euro. J. Mech. B/Fluids 31 30-43 (2012). The flow is assumed to be inviscid but vortical, with approximations on the vertical velocity and acceleration at the surface. These shallow water equations are simulated using an implicit finite-difference scheme. Examples of numerical experiments performed with this code are simulations of coupled translation-rotation forcing, and sloshing on model for the London eye (see below for a special code for this latter case).


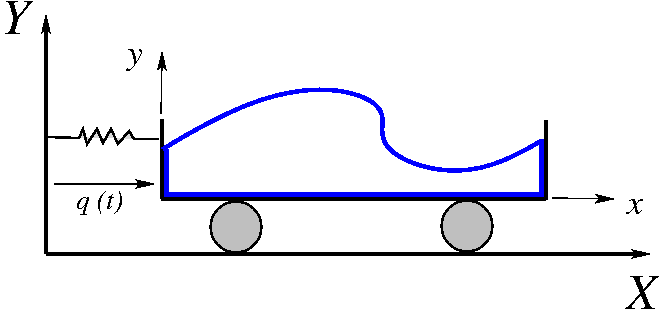
Matlab codes for dynamic coupling
This Matlab code solves the shallow-water equations coupled to vehicle motion. The equations are derived in Euro. J. Appl. Math. 21 479-517 (2010). The shallow water equations are transformed to the Lagrangian particle path description. Then coupling with the vehicle motion is determined by a variational principle. The Lagrangian functional is discretized using a variational integrator. The discrete finite-dimensional set of equations is then solved using the Stormer-Verlet method. Separate codes for the linear and nonlinear simulations are given below.

Matlab codes for London Eye simulations
This Matlab code solves the shallow-water equations for a vessel on the London Eye, including rotation of the vessel about its suspension point.